About me
I am a researcher at Toyota Central R&D Labs,. Inc. I received a B.E. degree in engineering from Osaka University in 2014, an M.S. degree in informatics from Kyoto University in 2017, and a Ph.D. degree in mathematical science from the University of Tokyo in 2024. My current research interests include controlling large-scale multi-agent systems and solving high-dimensional partial differential equations.
From September 2025 to August 2027, I will be staying at Imperial College London as a Sponsored Researcher. During this period, my company email address will not be available. Please contact me at my private address.
Work Experience
2017 Apr – Present: Toyota Central R&D Labs., Inc. in Aichi, Japan
- Numerical methods for PDEs arising in optimal control problems
- Controller design for very large-scale systems
- Exploring applications of quantum annealing machines for control engineering
- etc…
2016 July – 2017 Mar: Kyoto University in Kyoto, Japan
- Teaching Assistant of Complex Analysis Class
2015 July – 2016 Mar: Siemens Industry Software N.V in Leuven, Belgium
- Motion Controller Design for Airbus A330 based on 1-D & 3-D Co-simulation
2014 July: Mitsubishi Heavy Industries, Ltd. in Kobe, Japan
- Development of a Nuclear Power Plant Simulator
Education
2021 Apr - 2024 Mar: Ph.D. student at Graduate School of Mathematical Sciences, the University of Tokyo
- Thesis: Numerical Methods for Nonlinear Partial Differential Equations Arising from Large-Scale Multi-Agent Control Problems (Dean’s Award)
2014 Apr – 2017 Mar: Master of Informatics at Graduate School of Informatics, Kyoto University
- Thesis: Stability Analysis of Networked Monotone Systems
2010 Apr – 2014 Mar: Bachelor of Engineering at Department of Engineering Science, Osaka University
- Thesis: Stationary performance evaluation of control systems with random dither quantization
Skills
- General Programming: Python, C, C++, Julia, Matlab
- Operating System: Windows, macOS, Linux (Debian, Ubuntu)
- Embedded System: Raspberry Pi, Arduino, Simulink, ROS
- Numerical Methods: FreeFEM++, FEniCS
- Optimization: Gurobi, D-Wave
- Language: Japanese, English
My research
I am interested in modeling and control of large-scale dynamical systems. The following are descriptions of some of the published research topics I have worked on.
Controlling population dynamics using mean-field games (2019 – Present)
When controlling a large system, the larger the number of control targets, the longer it takes to compute the appropriate control inputs. To address this problem, we focus on a concept called the mean-field game, which approximates the optimal control system for a large number of populations. In mean-field games, “one-to-one” interactions are approximated as “one-to-population,” which leads to a reduction in computational complexity. Meanwhile, the mean-field game itself is also a system of equations that is difficult to solve in ordinary calculations, so it is necessary to develop a sophisticated numerical method. We investigate methods to numerically compute these mean-field games with high speed and high accuracy.

Animation of a group of 1000 agents controlled by the proposed control law. Each agent moves from bottom-left to top-right to minimize its associated cost function.
Reference
D. Inoue, Y. Ito, T. Kashiwabara, N. Saito, and H. Yoshida, “Model Predictive Mean Field Games for Controlling Multi-Agent Systems,” IEEE International Conference on Systems, Man, and Cybernetics (SMC), 2021
Controlling population dynamics using optimal transport (2020 – Present)
The problem of transporting a distributed object from one location to another with minimum cost is called the optimal transport problem. Although optimal transport is an old concept, its connection to control engineering is relatively new. We proposed a new control method by revisiting the multi-agent covering control problem with the concept of optimal transport. This method is an extension of existing methods in the sense that it is equivalent to existing covering control methods by fixing certain parameters. Numerical calculations show that the proposed method is superior to the existing method in terms of covering performance.

Animation of a group of 25 agents controlled by the proposed control law. The black dots represent the positions of the agents.
Reference
D. Inoue, Y. Ito, and H. Yoshida, “Optimal Transport-based Coverage Control for Swarm Robot Systems: Generalization of the Voronoi Tessellation-based Method,” in IEEE Control Systems Letter, 2020
Control applications of quantum computers (2018 – Present)
Recently, a new variant of quantum computers, called quantum annealing machines, has begun to be used commercially. Although its performance as a computer is not yet satisfactory, it is expected to improve in the future. Since annealing machines are limited in the form of problems they can solve, we are studying the transformation of seemingly unsolvable problems into solvable forms with approximations and variable transformations. We have proposed methods for solving model predictive control and traffic signal control problems using such transformations and have shown that the proposed methods are superior to some classical methods.
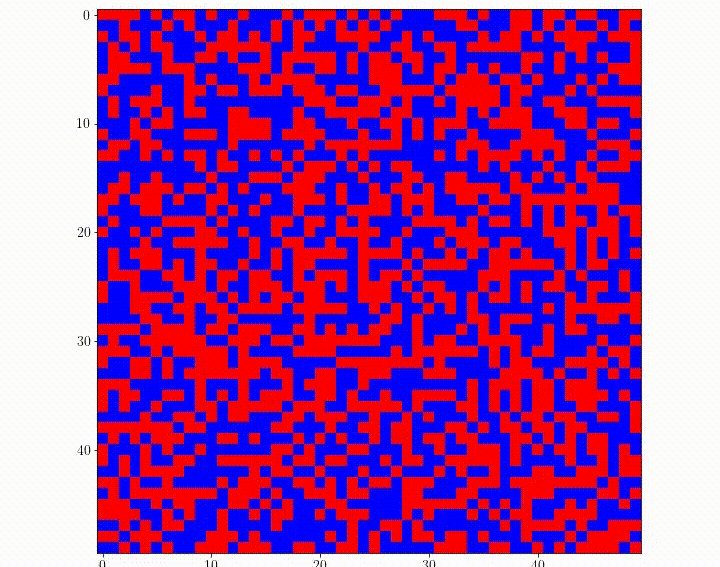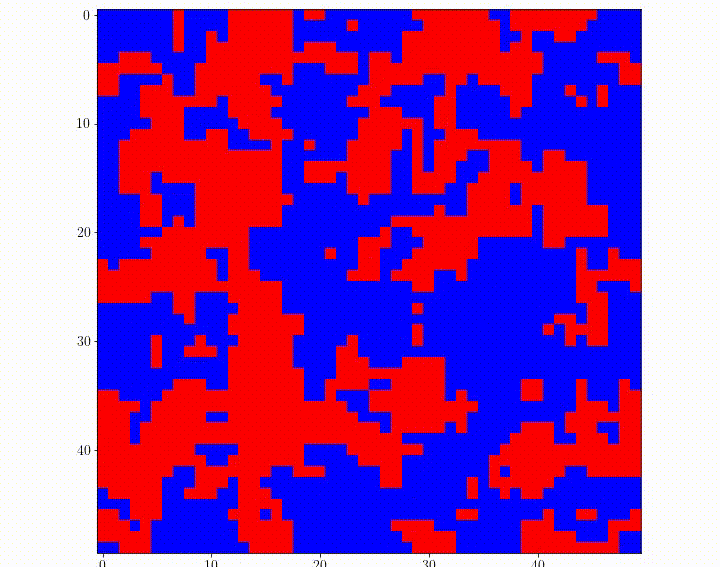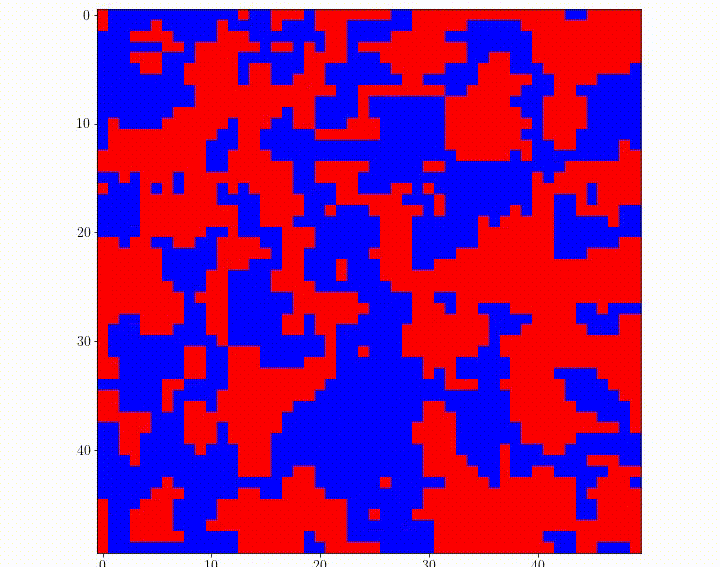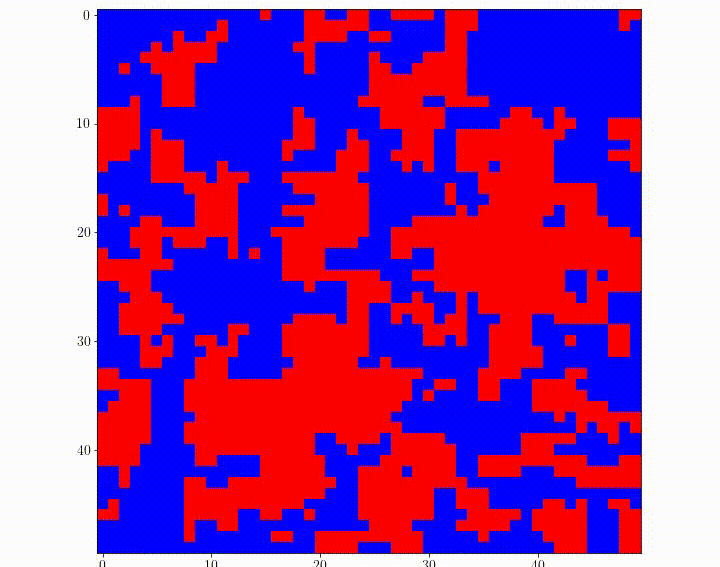
Animation of traffic lights at each intersection of a grid city, controlled by a quantum annealing machine. Red indicates that the intersection allows north-south traffic, and blue indicates that the intersection allows north-south traffic.
References
D. Inoue, H. Yoshida, “Model Predictive Control for Finite Input Systems using the D-Wave Quantum Annealer”, Scientific Reports, 10(1), 2020
D. Inoue, A. Okada, T, Matsumori, K. Aihara, H. Yoshida, “Traffic Signal Optimization on a Square Lattice with Quantum Annealing”, Scientific Reports, 11, 3303, 2021
Stochastic control of populations learned from living organisms (2018 – Present)
Organisms that are supposed to have no intelligence, such as ants and E. coli, can exhibit surprisingly intelligent behavior as a group. We are studying control algorithms that mimic the behavior of such organisms. In particular, we are developing a method to make agents act stochastically so that the group can form a desired shape.

Animation of 5,000 agents moving with the proposed method. Each agent only moves stochastically according to a simple algorithm, but they form an arbitrary shape as a group.
Reference
D. Inoue, D. Murai, and H. Yoshida, “Stochastic Self-Organizing Control for Swarm Robot Systems”, The Tenth International Conference on Swarm Intelligence (ICSI 2019), Chiang Mai, pp. 405-416, 2019.
Stability analysis of monotone systems (2015 – 2017)
The study of whether a system has a unique stable equilibrium point for all initial values is called a global stability analysis. This is easy to do when the system is linear, but it becomes extremely difficult when the system is nonlinear. Meanwhile, nonlinear systems such as biological population models and gene network models have a property called monotonicity, which allows us to determine their global stability by using a tool called the fixed point theorem. Previously, the global stability of systems with multiple interacting monotone systems has not been thoroughly analyzed. We have used techniques such as graph contraction to provide sufficient conditions of stability for some classes of these systems.
Reference
井上 大輔, 東 俊一, 杉江 俊治, ネットワーク化単調システムの安定性解析, 計測自動制御学会論文集, 2017, 53 巻, 9 号, pp. 493-500
Performance analysis of dithered quantized systems (2014 – 2016)
When sensors and actuators in a control system have a low resolution or when communication capacity is limited, continuous-valued signals are forcibly approximated to discrete-valued signals, which leads to performance degradation. Approximation to discrete values is called quantization, and it is known that performance can be slightly improved by intentionally applying a random number before quantization, which is called dither quantization. Although the improvement achieved by dither quantization has only been quantified experimentally, we have characterized this performance as the solution of a simple algebraic equation, using a technique called stochastic linearization.
References
K. Kashima and D. Inoue, “Replay attack detection in control systems with quantized signals,” 2015 European Control Conference (ECC), Linz, pp. 782-787, 2015.
K. Kashima and D. Inoue, “Stationary performance evaluation of control systems with random dither quantization,” 2014 European Control Conference (ECC), Strasbourg, pp. 1625-1630, 2014.